Data: 14/09/16
 
Presentes: Gislaine, Diego, Graça, Karina Fernandes, Daniel, Thamires, Alessandra, Dora e Laís (via Skype)
 
          Iniciamos o encontro de hoje com o desafio de mexer numa das fragilidades apresentadas por praticamente todos, senão, todos os participantes do GEProMAI: a álgebra. O texto referência para iniciarmos a discussão foi: “Álgebra no Ensino Básico” de João Pedro da Ponte, Neusa Branco, Ana Matos... que a princípio traz uma parte histórica e um tanto mais teórica do assunto, dando uma sensação de que tudo continuará nebuloso. Há que se considerar que é um texto em português de Portugal, portanto, um tanto mais instigante de ler, pois as construções linguísticas são um pouco diferentes.
          Parte do grupo teve essa percepção de um texto mais teórico e não tão direto. Alessandra chama atenção para a parte lida. Nesta parte inicial, os autores fazem um resgate histórico mesmo e coloca de uma maneira mais técnica a abordagem do pensamento algébrico no ensino. Segundo Alê, nos demais capítulos, as nuvens vão se dissipando e passamos a entender melhor a abordagem feita pelos autores, compreendendo melhor o que é a álgebra.
           Afinal, “o que é álgebra?” Indaga Dora. E aí que as coisas se complicam....rs. Adentramos muito timidamente nesse universo cheio de dúvidas e descobertas. Daniel, entende por álgebra a maneira como tratamos os números, nas relações que estabelecemos cotidianamente. Dora diz que a álgebra veio para fazer a generalização ao contrário da aritmética. Alguns exemplos começam a ser citados como o número irracional – número que não tem periodicidade, como o PI, por exemplo versus números complexos.
          Alê fala sobre os aspectos de redução – análise infinitesimal – entre 0 e 1 há quantos números? Os autores trazem uma questão de raciocínio, regularidades, se apropriar de elementos que não são só numéricos, é um processo mental, não é só numérico. Contexto de pensar sequências, o que caracteriza a álgebra? No quinto ano, a equação do 1º grau.
          Trabalhar as ideias de igual. Usamos o sinal de igual como operador, mas na álgebra, usamos o mesmo sinal com a ideia de igualdade.
Dora - Pensar o sinal de igual como algo que se refere a equivalência faz toda a diferença. Exemplo:

​

3 + 5 = 8                                              3 + 5 = x                                                 2x + 13 = x - 4

3 + 5 + 2 = 8 + 2                                3 + 5 + 2 = x + 2                         2x + 13 – 13 = x – 4 – 13

2x = x - 17                                      2x – s =  x – x – 17                                      x = -17

​

​

          Dúvida = A álgebra é o conteúdo ou só a sistematização? É uma espécie de técnica?
          Ale fala que a álgebra entra no sistema de numeração. Você pode trabalhar com equações que entram no sistema de numeração e sistematiza porque organiza o pensamento. 

          Pensar e resolver o problema utilizando símbolos convencionais?

          Pensamento concreto. Álgebra é um bloco da matemática. Todos os blocos envolvem o sistema de numeração. A geometria pode ou não envolver a álgebra. Área do quadrado, por exemplo e de um quadrado qualquer. A álgebra atrelada a geometria tem suas funções. Ela vem ajudar para fazer generalizações, criar padrões.

          Alê aponta que nos documentos da BNCC para os anos iniciais, há uma indicação para usar o quadriculado para medir a área, mas não falamos de sistematização. Existe um processo organizado, sem que eu tenha que fazer de maneira mais simples e mais demorado.

O pensamento algébrico é a vivência de muitas experiências para desenvolver padrões que possam ser generalizados.

          Graça comenta de uma atividade de sequência de formas e cores. É preciso que as pessoas percebam que existe um padrão e este, possibilita que eu coloque qualquer peça, a partir de uma posição, porque o padrão já está estabelecido. Trabalha com a posição par e ímpar.

           Laís questiona sobre uma atividade já realizada por alguns participantes do grupo com algumas crianças - atividade dos três canudos. É pensamento algébrico? Dora diz que depende da maneira como conversamos com as crianças. O que acontece se eu dobrar um lado? E dois?

           Karina sugere a leitura das partes que cada um destacou no texto. Alê inicia com destaques da página 42. Pontilhados para formar triângulos. Quando vamos fazer uma operação 3 + 7 = 10 + 1 = 11. O algoritmo é técnico, mas não é matemático, pois é preciso trabalhar as relações dos números mais do que, simplesmente, trabalhar a técnica algébrica.

           Dora comenta que a busca de padrões é uma forma de pensamento algébrico.

         

Exemplo: Laís = soma dos dois lados maior que outro é um exemplo de pensamento algébrico.

​

Dora – números muito grandes ou muito pequenos é a ideia de número infinitesimal.

Alê – números naturais – aquilo que é natural contar.

Dora - A fração veio logo em seguida, e os números negativos.

Graça – atividade de ligar – juntar quantidades que estão sendo representadas por figuras, pontos, números. Precisam rever, refazer, conversar várias vezes. A função da álgebra é de relacionar duas coisas.

​

          Relembrando conceitos... As equações são colocadas em potências. Fórmula de Báskara.  Quando não há expoente está elevado a primeira potência. Quando vai aumentando o expoente, vai aumentando os graus das equações e também o número de resoluções.

Diego entende a álgebra como forma de resolução, de generalização. Chama atenção para o fato de só executamos a fórmula, por isso, o não entendimento.

          Alê traz outros exemplos do pensamento algébrico que muitos de nós já utilizou como relações de conjunto = pertence, não pertence, contém, está contido; diz que isso se perdeu um pouco. Medimos área com 1 quadradinho, vou chegando às possibilidades de ir e vir de construção do pensamento.

          Dora fala da álgebra enquanto equação: que é uma sentença matemática aberta (porque tenho um valor desconhecido), expressa por uma igualdade. A equação não é uma expressão algébrica. Acredita na potencialidade de trabalhar com o não, com a negativa. Por que não pode ser o número 10? Também atenta para os trabalhos com números não inteiros. 17/4.

          Alê faz uma analogia da álgebra com uma balança de dois pesos - busca ficar equilibrada.

Graça fala da função = uma coisa em função da outra. Levar três pães depende do valor do pão e o quanto ele custa. Outros exemplos = ida ao clube – ter sol. O que eu consigo controlar a relação de ter sol e eu ir no clube. Estabelecer relações, por exemplo, quantas vezes fui ao clube este mês.

          Alê dá um exemplo sobre o valor pago pela primeira hora num estacionamento e o valor pago pelas demais horas.

Dora exemplifica com o jogo de futebol. Proporcionalidade entre tempo de jogo e placar. Função, qualquer coisa que tem relação com a outra é uma função, mas não necessariamente uma função matemática.

          Modelação matemática – tirar fotos de prédios e encontrar alternativas para fazer uma pessoa cadeirante ter acesso a andares superiores. Nesse exemplo, seria a construção de rampas. Colocar a matemática a partir de modelos reais. D’ambrózio(?) Hod (?) Exemplo, extração do mel da abelha. Modelava um modo de extração para as abelhas produzirem mais mel, ou seja, criava um padrão.

Diego e Graça apresentaram o texto – Pensamento algébrico nos primeiros anos iniciais

          Álgebra “é, sobretudo, um modo de pensar, um método para ver e expressar relações.”

          Atividade do cumprimento – 10 crianças se cumprimentando. Há um pensamento algébrico? Não, é apenas uma contagem. Mas, posso perguntar: e se fossem 15 crianças? Ou 50? Se elas repetirem tudo de novo, não houve um pensamento algébrico. O suporte dela é o registro, uma espécie de tabela, resumo. A partir desse registro, você pode dizer que houve pensamento algébrico. “Se um aluno descrever como se pode obter o total de apertos de mãos, independentemente do número de pessoas, ou seja, se passa à generalização, dizemos que pensou algebricamente (Alvarenga e Veiga, 2007).

          Pensamento algébrico versus pensamento matemático.

          Nem todo pensamento algébrico é matemático, mas nem todo pensamento matemático é algébrico. Isso é álgebra, destacou o Diego.

 

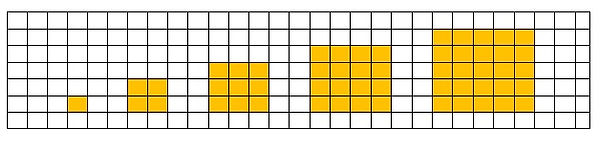
Graça – atividade dos quadradinhos

​

 

 

 

 

 

 

 

 

​

 

 

 

 

 

 

 

 

 

 

 

​

​

​

1         3         5         7         9         11       13       15       17

 

5 X 3 + (5-3)...

10 X 3 + (10 – 3)

​

​

​

​

​

​

​

​